Mongal Saha
As we explore our surroundings in Nature more and more, we notice that several facts and observations can be described mathematically. A strong correlation is observed between Nature and mathematics. According to the famous mathematician Euclid, “The laws of Nature are but the mathematical thoughts of God”. Mathematics is all around us. Mathematical formulations and justifications are inherent in our universe; in plants, animals, geographical observations, fractals, shapes and patterns and, many more.
There are many examples in the world of plants. A few examples include the number of spirals in a pine cone or a pineapple, the seeds in a sunflower, the number of petals and the symmetry of a flower, etc. Concentric circles are observed in the layers of onions and the rings of trees that form as the tree grows and ages.
Mathematical symmetry is inherent everywhere in Nature. The human body would be an excellent example of a living being that has symmetry. A dihedral five symmetry is observed in a starfish’s body structure with five rotations of 72 degrees each, and with five lines of reflection. Hexagons are six-sided polygons that fit most closely together without any gaps. The hexagonal structure of wax cells that bees create to store their eggs and larvae is an excellent example of mathematical optimisation of space.
Many birds follow their flight path using celestial objects like the sun or stars, and unconscious trigonometric calculations to navigate their flight. Birds solve critical trigonometric problems in the same way a waterfall follows the Navier-Stokes equation or a dog finds an object.
Natural objects have some definite shapes. Geometry is the branch of maths that describes the shapes of many natural objects. For example, cones are formed by volcanoes. The steepness and height of the cones depend on the runniness (viscosity) of the lava. Fast, runny lava forms flatter cones, but the thick viscous lava forms steep-sided cones. Cones are three-dimensional solids whose volume can be calculated as (1/3 x area of base x height).
The building blocks of the natural world can easily be explained in terms of some mathematical formulations. A fractal is a never-ending recursive pattern where the same basic shape is repeated again and again in the shape itself. They are another intriguing mathematical structure that is observed in Nature. Fractals make up many aspects of our world, including the leaves of ferns, the branches of trees, the branching of neurons in our brains, and coastlines.
Mathematics helps to interpret all the activities of our brain. When information is being processed, governed by a set of patterns like those found in the branches of a tree or the fluid dynamics of a waterfall, the way it feels is consciousness. Basically, consciousness is a mathematical pattern. These are a few of my favourite examples of maths found in Nature, but many other stones are left unturned.
We can understand the order of the universe by studying the patterns that emerge from it. Even something that we see randomly as the shape of a tree’s branches has an order. The main trunk of a tree will grow until it produces a branch that has two growth points and each stem branches into two. Interestingly, this pattern is repeated for every new stem.
The Fibonacci sequence is a unique mathematical sequence followed by Nature herself. It was proposed by famous mathematician Leonardo Pisano Fibonacci, who is popularly known as Fibonacci. This sequence is a peculiar series of numbers from classical mathematics that has found application in advanced mathematics, Nature, statistics, computer science, etc. It may be treated as a fundamental sequence because it can explain several natural phenomena. Surprisingly, it is observed that numerous natural facts follow this sequence and can be thought of as the best secret code of Nature. It can well explicate the dimensions of the Pyramids of Giza, the vast sea shells, famous paintings, famous architectural designs, and many more.

The Fibonacci sequence is a series of numbers starting with 0 and 1 and the sum of the two preceding numbers form the next number. The mathematical rule to find any Fibonacci number (F) of the sequence is:
Fn = Fn–1 + Fn–2
Where F1 = 0, F2 = 1, n > 3
The simplest sequence is: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…
The average ratio of every two consecutive terms in the Fibonacci sequence gives us a famous constant, popularly known as the golden ratio and denoted by f, where f =1.618033989....... We can find examples of the golden ratio everywhere in Nature. This aesthetically appealing ratio is found in geometrical shapes, plant structures, drawings and paintings, architectural designs, and even in the field of financial activity. There are many other examples in our surroundings to be explored.
This work is an initiative in this direction. It aims to search some new natural examples in our surroundings where the golden ratio is applicable. As a part of empirical studies, here is a case example regarding the connotation of the Fibonacci sequence and the golden ratio with the pattern of flower petals and leaf structure of some commonly available plants in the different areas of Assam, India.

Empirical studies
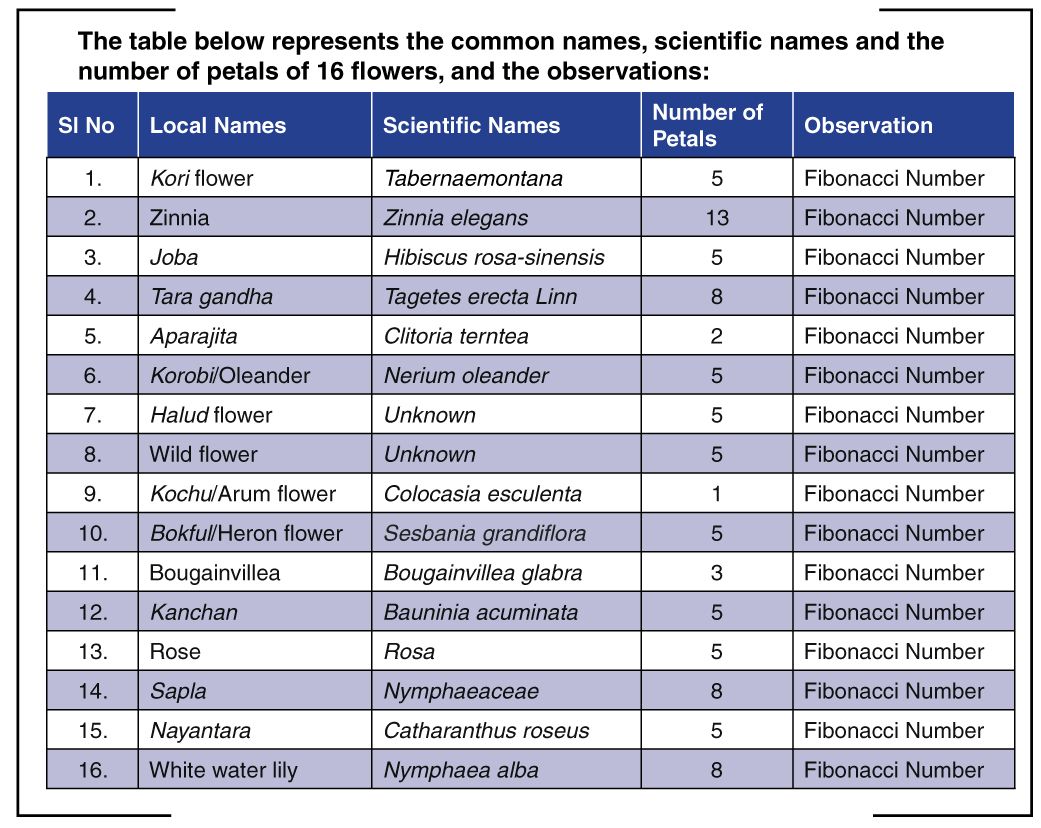
Case example 1: The Fibonacci sequence and the pattern of flower petals
In Nature, the flowers of different species have some definite patterns and number of petals. An exciting relation is observed between the Fibonacci sequence and the structure of petals of some common flowers. The number of petals is equal to a term of the Fibonacci sequence: 0, 1, 1, 3, 5, 8, 13, 21…
Conclusion: This study presents only one case study regarding the relation between the two kingdoms, mathematics and plants. The beauty of mathematics is that it seems to be inherent in plants. The empirical study shows how the Fibonacci sequence is beautifully followed by the flower petals. A fascinating observation is that maximum flowers have five petals. Most probably, it is due to the fact that the pentagon structure is one of the most stable structures. Obviously, some exceptions are present everywhere to establish regularity.
(National Teacher’s Awardee-2009,
[email protected])